箱形图（Box-plot）又称为盒须图、盒式图或箱线图，是一种用作显示一组数据分散情况资料的统计图，因形状如箱子而得名。它主要用于反映原始数据分布的特征，还可以进行多组数据分布特征的比较。

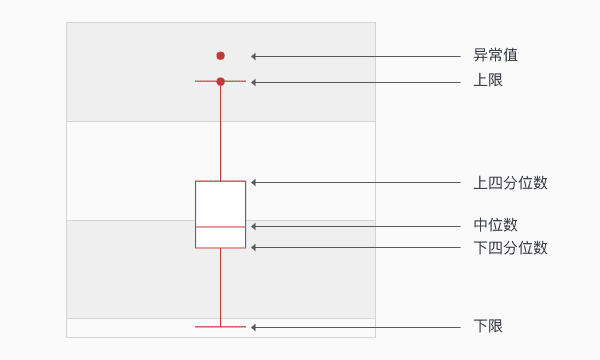
箱形图于1977年由美国著名统计学家约翰·图基（John Tukey）发明。主要包含六个数据节点，将一组数据从大到小排列，分别计算出他的上边缘，上四分位数Q3，中位数，下四分位数Q1，下边缘，还有一个异常值。

箱型图

绘制步骤

  1. 画数轴，度量单位大小和数据集的单位一致，起点比最小值稍小，长度比该数据集的极差稍长。
  2. 画一个矩形盒子，两端边的位置分别对应数据集的上下四分位数（Q3和Q1）。在矩形盒内部中位数位置画一条线段为中位线。
  3. 在Q3+1.5IQR和Q1-1.5IQR处画两条与中位线一样的线段。这两条线段为异常值截断点（上下限），称其为内限；在Q3+3.0IQR和Q1-3.0IQR处画两条线段，称其为外限。处于内限以外位置的点表示的数据都是异常值，其中在内限与外限之间的异常值为温和的异常值（mild outliers），在外限以外的为极端的异常值(extreme outliers)。四分位距IQR=Q3-Q1。
  4. 从矩形盒两端边向外各画一条线段直到不是异常值的最远点（上下限），表示该批数据正常值的分布区间。
  5. 用“〇”标出温和的异常值，用“*”标出极端的异常值。相同值的数据点并列标出在同一数据线位置上，不同值的数据点标在不同数据线位置上。至此一批数据的箱形图便绘出了。

参考资料