机器学习之集成方法
Contents
单个学习器很容易会出现过拟合 or 欠拟合问题。为了提高学习器的泛化能力,可以采取一定的策略构建并结合多个学习器来完成学习任务 – 集成学习(Ensemble Learning),有时也被称为多分类器系统(multi-classifer system)、基于委员会的学习(committee-based learning),都是为了描述多个学习器共同作用。
个体学习器与集成学习
个体学习器(Individual learner)
通常由一个现有的学习算法从训练数据产生,例如C4.5决策树算法、BP神经网络算法等。
集成学习
根据不同类型个体学习器的组合方式可以分为:同质(homogeneous)集成和异质(heterogeneous)集成。
- 同质集成:只包含同种类型的个体学习器。同质集成中的个体学习器称为 基学习器(base learner),相应的算法称为 基学习算法(base learning algorithm)。
- 异质集成:包含不同类型的个体学习器。个体学习器称为 组件学习器(component learner)。
考虑一个简单例子:在二分类任务中,假定3个分类器在测试样本上的表现如图8.2所示,其中✅表示分类正确,❎表示分类错误,集成学习的结果通过投票法产生,少数服从多数。

- (a):每个分类器只有66.6%精度,集成学习精度达到了100%
- (b):3个分类器没有差别,集成之后性能没有提高。
- (c):每个分类器精度都只有33.3%,集成学习之后的结果变得更糟。
结论:要获得好的集成,个体学习器应 好而不同,即个体学习器要有一定的 准确性(a, c)学习器不能太坏,并且要有 多样性 (b中学习器没有多样性)学习器间具有差异。
集成学习通过将多个学习器进行结合,常常可以获得比单一学习器显著优越的泛化性能。这对 弱学习器(weak learner) 尤为明显。
- 弱学习器:常指泛化性能略优于随机猜测的学习器。例如,二分类问题上精度略高于50%的分类器。
集成学习方法
根据个体学习器的生产方式,目前的集成学习方法大致可以分为两类:
- Boosting:个体学习器之间存在强依赖关系,必须串行生成的序列化方法。
- Bagging and Random Forest:个体学习器之间不存在强依赖关系,可同时生成的并行方法。
Boosting
工作机制:先从初始训练集训练出一个基学习器,再根据基学习器的表现对训练样本分布进行调整,使得先前基学习器做错的训练样本在后续受到更多关注,然后基于调整后的样本分布来训练下一个基学习器;如此重复进行,直到基学习器数目达到事先指定的值T,最终将这T个基学习器进行加权结合。
Boosting是一族可将弱学习器提升为强学习器的算法。最著名的代表是 AdaBoost。

从偏差-方差分解的角度看,Boosting 主要关注降低偏差,因此 Boosting 能基于泛化性能相当弱的学习器构建出很强的集成。标准AdaBoost只适用于二分类任务。
Bagging 与 Random Forest
从前面可知,如果想得到泛化性能强的集成,集成中的个体学习器应尽可能相互独立。虽然 独立 在现实任务中无法得到,但可以设法使基学习器尽可能具有较大的差异。
给定一个训练数据集,为了获取有差异的基学习器,一种可能的做法是对训练样本进行采样,产生出若干个不同的子集,再从每个数据子集中训练出一个基学习器。由于训练数据不同,我们获得的基学习器有望具有比较大的差异。同时,为了保证个体学习器不能太差,即训练数据子集尽可能大,我们采用相互有交叠的采样子集。
#####Bagging
Bagging 是并行式集成学习方法最著名的代表。
给定包含m个样本的数据集,我们先随机取出1个样本放入采样集中,再把该样本放回初始数据集,使得下次采样时该样本仍有可能被选中,这样经过m次随机采样操作,我们得到包含m个样本的采样集,初始训练集中有的样本在采样集里多次出现,有的从未出现,理论上有63.2%的样本出现在采样集里面。这称之为 有放回重复采样(bootstrap sampling)。
基于 有放回重复采样,我们可以采样出T个含有m个训练样本的采样集,然后基于每个采样集训练一个出一个基学习器,再将这些基学习器进行结合,这个方法称为 Bagging集成。
- 对分类任务使用简单投票法,如有票数相同情况,随机选择一个,也可以进一步考察学习器投票的置信度来确定。
- 对回归任务使用简单平均法。

与标准AdaBoost只适用于二分类任务不同,Bagging能不经修改地用于多分类、回归任务。
有放回采样的另一个优点是:剩余的36.8%的样本可用作验证集对泛化性能进行 包外估计(out-of-estimate)。
从 偏差-方差分解的角度 看, Bagging 主要关注降低方差。因此它在不剪枝决策树、神经网络等易受样本扰动的学习器上效果更为明显。
Random Forest
随机森林(Random Forest)是 Bagging 的一个扩展变体。RF 在以决策树为基学习器构建 Bagging 集成的基础上,进一步在决策树的训练过程中引入了随机属性选择。
具体来说,传统决策树在选择划分属性时是在当前节点的属性集合(假定有$d$个属性)中选择一个最优属性;而在RF中,对基决策树的每个结点,先从该结点的属性集合中随机选择一个包含$k$个属性的子集,然后再从这个子集中选择一个最优属性用于划分。这里的参数k控制了随机性的引入度:若令 $k=d$,则基决策树的构建与传统决策树相同;若令 $k=1$,则是随机选择一个属性用于划分;一般情况下,推荐值 $k=log_2d$。
随机森林简单、容易实现、计算开销小,在很多现实任务中展现出更强大的性能,被誉为 “代表集成学习技术水平的方法”。
随机森林对Bagging只做了小改动,但是与Bagging中基学习器的 多样性 仅通过样本扰动(通过对初始训练集采样)而不同,随机森林中基学习器的多样性不仅来自样本扰动,还来自属性扰动,这就使得最终集成的泛化性能可通过 个体学习器之间差异度的增加(核心) 而进一步提升。
组合策略
学习器结合可能会从3各方面带来好处:
- 单个学习器可能因误选而导致泛化性能不佳,结合多个学习器则会减少这一风险(统计角度)
- 学习算法往往会陷入局部极小,有的局部极小点所对应的泛化性能可能很糟糕,而通过多次运行之后进行结合,可降低陷入糟糕局部极小点的风险(计算角度)
- 某些学习任务的真实假设可能不在当前学习算法所考虑的假设空间中,此时若使用单学习器肯定无效,而通过结合多个学习器,由于相应的假设空间有所扩大,有可能得到更好的近似(假设空间角度)
平均法
对 数值型输出 ,最常见的结合策略是使用平均法(averaging)。
-
简单平均法(simple averaging)
$H(x)=\frac{1}{T}\displaystyle\sum_{i=1}^{n}h_i(x)$
-
加权平均法(weighted averaging)
$H(x)=\displaystyle\sum_{i=1}^{n}w_ih_i(x)$
其中 $w_i$ 是个体学习器 $h_i$ 的权重
通常要求:$w_i\geq0,\displaystyle\sum_{i=1}^{n}w_i=1$
集成学习中的各种结合方法都可视为其特例or变例。事实上,加权平均法可认为是集成学习研究的基本出发点,对给定的基学习器,不同的集成学习方法可视为通过不同的方式来确定加权平均法中的基学习器权重。
####投票法
对 分类 任务来说,最常见的结合策略是使用投票法。学习器 $h_i$ 将从类标记集合 ${c_1, c_2, …, c_N}$ 中预测出一个标记。将 $h_i$ 在样本上的预测输出表示为一个N维向量 $(h_i^1(x),h_i^2(x),…,h_i^N(x))$ 其中 $h_i^j(x)$ 是 $h_i$ 在类别标记 $c_j$ 上的输出。
-
绝对多数投票法(majority voting)
$H(x)=\begin{cases}c_j,\ if\ \displaystyle\sum_{i=1}^Th_i^j(x)>0.5\displaystyle\sum_{k=1}^N\sum_{i=1}^Th_i^k(x);\ reject,\ otherwise\end{cases}$
若某个标记的票过半数,则预测为该标记,否则拒绝预测。
-
相对多数投票法(plurality voting)
$H(x)=c_{arg\ max(j)\sum_{i=1}^Th_i^j(x)}$
预测为得票最多的标记,若同时有多个标记获最高票,则从中随机选取一个。
-
加权投票法(weighted voting)
$H(x)=c_{arg\ max(j)\sum_{i=1}^Tw_ih_i^j(x)}$
与加权平均法类似,$w_i$ 是 $h_j$ 的权重,通常 $w_i\geq0,\displaystyle\sum_{i=1}^Nw_i=1$。
将所有模型预测样本为某一类别的概率的平均值作为标准,概率最高的对应的类型为最终的预测结果,也称 加权投票法。
上面的投票方式没有限制个体学习器输出值的类型。在现实任务中,不同类型个体学习器可能产生不同类型的 $h_i^j(x)(第i个学习器对第j个样本的预测结果)$,常见的有:
- 类标记:$h_i^j(x)\in{0,1}$,若成功预测为1,否则为0.使用类标记的投票亦称 硬投票(hard voting)。
- 类概率:$h_i^j(x)\in[0,1]$,相当于对后验概率 $P(c_j|x)$ 的一个估计。使用类概率的投票亦称 软投票(soft voting)。
例子:
| A | B | |
|---|---|---|
| 模型1 | 99% | 1% |
| 模型2 | 49% | 51% |
| 模型3 | 40% | 60% |
| 模型4 | 90% | 10% |
| 模型5 | 30% | 70% |
后面百分比表示模型预测的概率。
-
Hard voting:A - 2票,B - 3票;最终结果为B。
-
Soft voting:
A - $(0.99+0.49+0.4+0.9+0.3)/5=0.616$
B - $(0.01+0.51+0.6+0.1+0.7)/5=0.384$
这里个体学习其权重都为 $1/5$ ,最终结果为A。
对比:Hard voting投票方式最终结果不是由概率值更大的模型1和模型4决定,而是由概率值相对较小的模型来决定。
学习法
当训练数据很多时,一种更为强大的结合策略是使用 学习法,即通过另一个学习器来进行结合。Stacking 是学习法的典型代表。
- 初级学习器:原始的个体学习器
- 次级学习器or元学习器(meta-learner):用于结合的学习器。
Stacking 先从初始数据集训练出初级学习器,然后 生成 一个新数据集用于训练次级学习器。初级学习器的输出被当作样例输入特征,而初始样本的标记仍被当作样例标记。
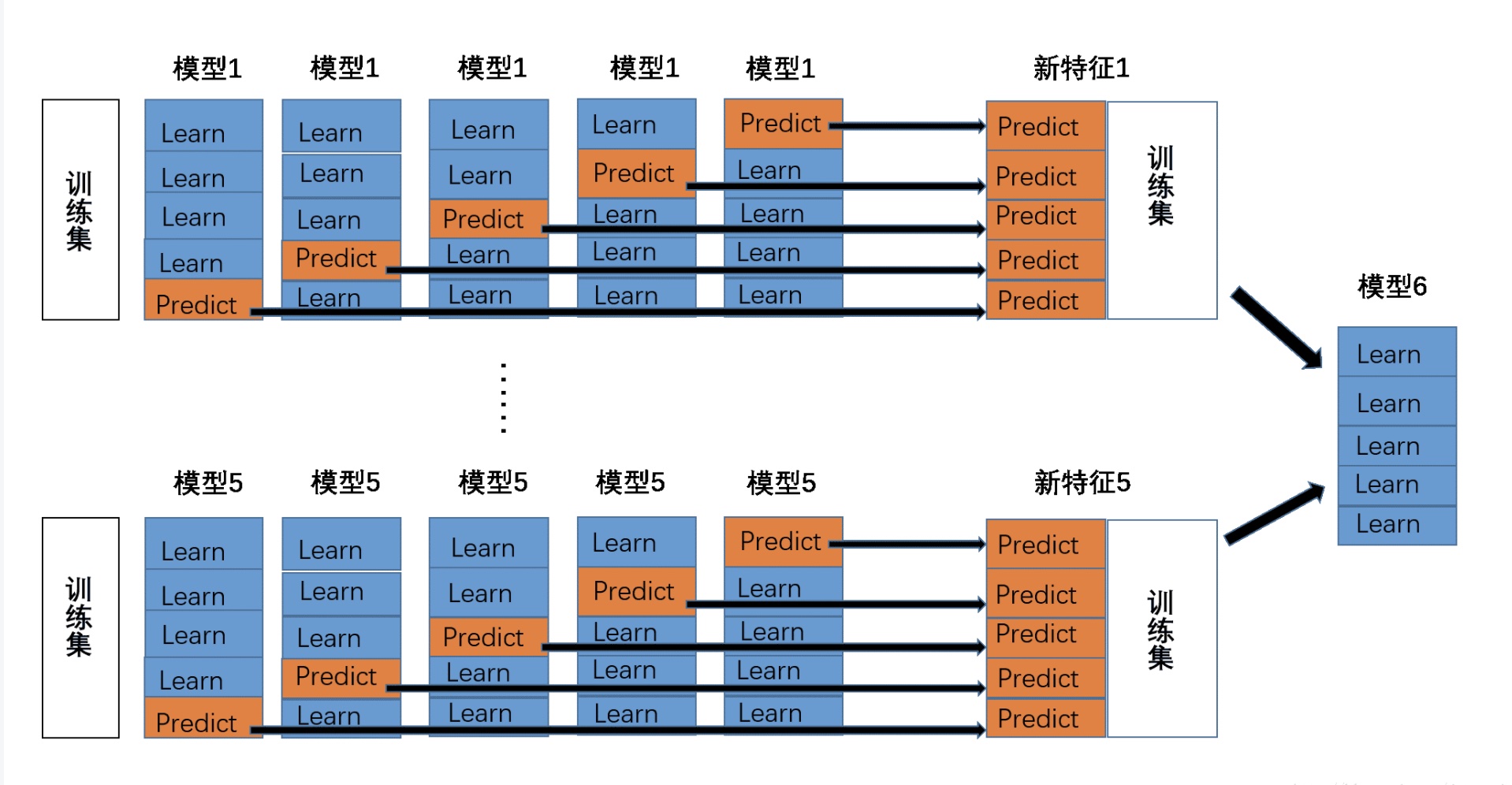
下面以K- Fold交叉验证为例:
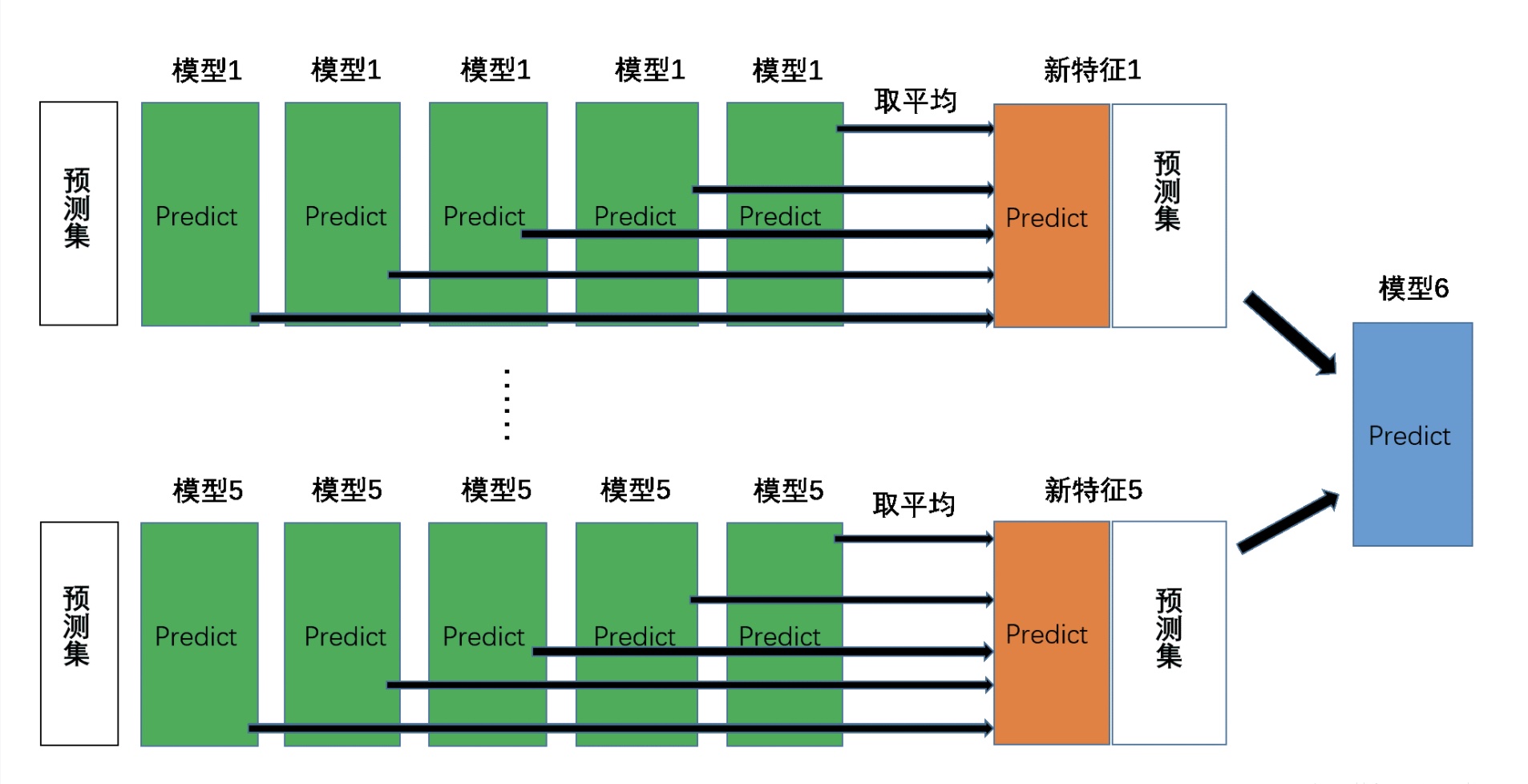
最后获得次级训练集为 $M(训练集样本个数)\times N(初始算法个数)$ 矩阵数据大小。
多样性
欲构建泛化性能强的集成,个体学习器应 好而不同。
误差-分歧分解(error-ambiguity decomposition) 表示个体学习器准确性越高、多样性越大,则集成越好。
多样性度量(diversity measure)
多样性度量是用于度量集成中个体分类器的多样性,即估算个体学习器的多样化程度。典型的做法是 考虑个体分类器的两两相似/不相似性。
给定数据集 $D={(x_1,y_1),(x_2,y_2),…,(x_m,y_m)}$,对二分类任务,$y_i\in{-1,+1}$,分类器 $h_i$ 与 $h_j$ 的预测结果列联表(contingency table)为:
| $h_i=+1$ | $h_j=-1$ | |
|---|---|---|
| $h_j=+1$ | $a$ | $c$ |
| $h_j=-1$ | $b$ | $d$ |
其中,$a$ 表示 $h_i$ 与 $h_j$ 均预测为正类的样本数目;$b,c,d$ 含义由此类推;$a+b+c+d=m$ 。基于这个列联表,下面给出一些常见的多样性度量。
-
不合度量(disagreement measure)
$dis_{ij}=\frac{b+c}{m}$
$dis_{ij}$ 的值域为 $[0,1]$,值越大则多样性越大。
-
相关系数(correlation coefficient)
$\rho_{ij}=\frac{ad-bc}{\sqrt{(a+b)(a+c)(c+d)(b+d)}}$
$\rho_{ij}$ 的值域为 $[-1,1]$。若 $h_i$ 与 $h_j$ 无关,则值为0;若 $h_i$ 与 $h_j$ 正相关则值为正,否则为负。
-
Q-统计量(Q-statistic)
$Q_{ij}=\frac{ad-bc}{ad+bc}$
$Q_{ij}$ 与 $\rho_{ij}$ 的符号相同,且 $|Q_{ij}|\leq|\rho_{ij}|$。
-
$\kappa-$统计量($\kappa-$statistic)
$\kappa=\frac{p_1-p_2}{1-p_1}$
其中,p1是两个分类器取得一致的概率;p2是两个分类器偶然达成一致的概率,它们可由数据集D估算:
$p_1=\frac{a+d}{m}$
$p_2=\frac{(a+b)(a+c)+(c+d)(b+d)}{m^2}$
若,分类器 $h_i$ 与 $h_j$ 在D上完全一致,则 $\kappa=1$;若它们仅是偶然达成一致,则 $\kappa=0$。$\kappa$ 通常为非负值,仅在 $h_i$ 与 $h_j$ 达成一致的概率甚至低于偶然性的情况下取负值。
多样性增强
在集成学习中需有效地生成多样性大的个体学习器。一般思路是在学习过程中引入随机性,常见做法主要是对数据样本、输入属性、输出表示、算法参数进行扰动。
-
数据样本扰动
给定初始数据集,可从中产出不同的数据子集,再利用不同的数据子集训练出不同的个体学习器。数据样本扰动通常是基于采样法。
- 效果明显:决策树、神经网络,对不稳定基学习器很有效。
- 效果不明显:线性学习、支持向量机、朴素贝叶斯、K邻近学习等,这样的基学习器称为 稳定基学习器(stable base learner)。
-
输入属性扰动
训练样本通常由一组属性描述,不同的 子空间(subspace),即属性子集提供了观察数据的不同视角。显然,从不同子空间训练出的个体学习器必然有所不同。
-
输出表示扰动
此类做法的基本思路是对输出表示进行操纵以增强多样性。可对训练样本的类标记稍作变动,如 翻转法(Flipping Output) 随机改变一些训练样本的标记;也可对输出表示进行转化,如 输出调制法(Output Smearing) 将分类输出转化为回归输出后构建个体学习器;还可将原任务拆解为多个可同时求解的子任务,如 ECOC法 利用纠错输出码将多分类任务拆解为一系列二分类任务来训练基学习器。
-
算法参数扰动
基学习算法一般都有参数需进行设置,例如神经网络的隐层神经元数、初始连接权值等,通过随机设置不同的参数,往往可以产生差别较大的个体学习器。
不同的多样性增强机制可同时使用,有些方法甚至同时使用了更多机制。