前言

二分法（Binary search）对于一个 已排序的对象 是一个很有效的算法。二分法可以理解为一个 动态的夹逼行为（夹逼定理） ，通过重复选择列表的中间值作为左or右的边界值，直到区间所包含的元素为1个。

当你向一个人去描述一个算法时，我们总会默认地忽略一些细节。比如，学习蛋糕烹饪，会默认你会打开冰箱，取出鸡蛋，打碎鸡蛋等操作。而且同时你或许还会填充一些细节，但是电脑程序不会这样，所以当我们设计一个电脑程序时，需要完全描述这个程序的实现过程。

  • 问题的输入是什么？
  • 需要的输出是什么？
  • 需要创建什么变量，它们的初始值是什么呢？
  • 中间步骤需要计算那些值？
  • 最终的计算机输出是什么？
  • 这些步骤中重复的地方是否可以用一个循环来简化？

猜数字游戏

Q：猜100以内某个数字（比如：52）。

Step1: 如果你猜25，我告诉你猜的值有点小

Step2: 如果你猜81，我告诉你猜的值有点大

Result1: 那么这个数字就是在 [26, 80]

二分法1

Figure1: 猜数字游戏示意图。

在每一次循环中，通过对猜测的数字做判断（猜大了or猜小了）来缩小找寻的数字区间：

[1, 100] => [26, 100] => [26, 82]

二分法

上面猜数字游戏中，26，82明显是随便猜测的数字，为了方便计算机的实现，一般猜测数字都是中间数字，将前面的数字区间分成两个区间大小相近的两个字区间。比如：如果现在的区间是 [26, 80]，那么下次你的猜测数字是 (26+82)/2 = 53，如果告诉你53还是高了，那么就可以排除 [53,82]，而留下 [26,52]。

对于一个包含$n$个元素的有序数组，查询数字为target，二分法步骤：

  1. 让 $min=0$，$max=n-1$（索引值）。
  2. **IF $max<min$ **，停止：target不在数组内。Return -1
  3. 计算 $min, max$ 平均值为：guess，四舍五入（rounded down）取整。
  4. IF array[guess] = target，停止：找到了目标值。Return guess。
  5. IF array[guess] < target, Set min = guess + 1。
  6. Else， array[guess] > target, Set max = guess - 1。
  7. 返回到Step 2。

二分法效率

我们知道，当遍历一个包含 $N$ 个元素的列表，查找target的时候最坏的情况下要做 $n$ 次 guess。如果使用二分法，最多需要做几次guess呢？

最关键的idea：每做一次不正确的guess，包含target的数据部分为上一步数据长度的1/2。假设初始的数据长度为32，那么第一次错误的guess会排除16个元素，第二次的错误guess会排出8个元素，然后4，然后2，然后1。

在最坏的情况下，总的排除元素个数为 $n$ 。根据等比数列公式有：$2^m+2^{m-1}+…+2^0=$N。所以我们会得到最差的次数为：**$log_{2}N$**。

二分法2

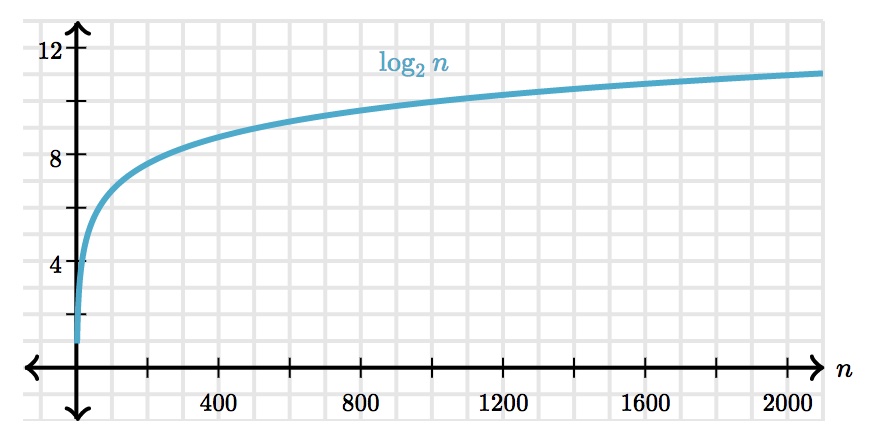
Figure2: Running time of Binary search

例子：搜索插入位置

####题目描述：

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

你可以假设数组中无重复元素。

示例 1:

1
2

输入: [1,3,5,6], 5
输出: 2

示例 2:

1
2

输入: [1,3,5,6], 2
输出: 1

示例 3:

1
2

输入: [1,3,5,6], 7
输出: 4

示例 4:

1
2

输入: [1,3,5,6], 0
输出: 0

解题思路：

根据题目描述，需要我们 按顺序 将目标值插入到一个数组里面。可以使用二分法来实现。

python代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

class Solution:
    def searchInsert(self, nums: List[int], target: int) -> int:
        left = 0
        right = len(nums)-1
        if nums[-1] < target:
            return len(nums)

        while left < right:
            mid = (left + right)//2 #取整
            if nums[mid] == target:
                return mid
            elif nums[mid] > target:
                right = mid
            else:
                left = mid + 1
        return left

参考：